Dans de nombreux systèmes physiques, on compare deux signaux sinusoïdaux. C’est ce que nous allons apprendre dans cette partie !
Déphasage et retard entre deux signaux sinusoïdaux
Un cas particulier fréquent est quand les signaux ont la même fréquence. Dans ce cas, on aime comparer le décalage entre les deux signaux.
Déphasage entre deux signaux de même fréquence
Définition
Le déphasage entre deux signaux est une mesure du décalage entre deux signaux sinusoïdaux de même fréquence. Si on dispose de deux signaux sinusoïdaux et de même fréquence :
alors le déphasage de par rapport à est la quantité :
Vocabulaire
Si est positif, le signal 2 est en avance de phase par rapport au signal 1.
Si est négatif, le signal 2 est en retard de phase par rapport au signal 1.
Cas particuliers de déphasage
Quelques valeurs de déphasage remarquables ont un nom particulier qu’il est utile de connaître.
Signaux en phase
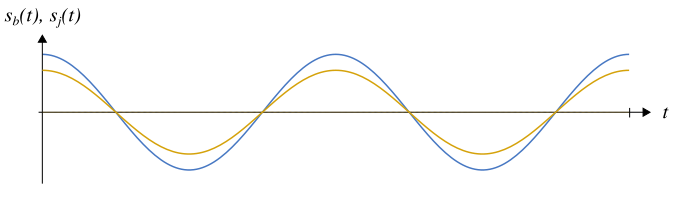
Quand le déphasage est nul, on dit que les signaux sont en phase. Dans cette configuration, leurs maximums et minimums coïncident ; les signaux oscillent conjointement.
Mathématiquement, cela signifie que les deux signaux sont proportionnels. C’est par exemple le cas pour la tension électrique aux bornes d’une résistance et le courant électrique qui la traverse.
Signaux en opposition de phase
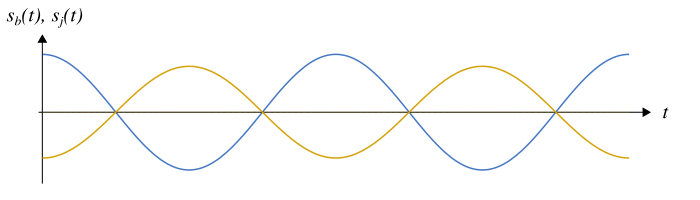
Quand le déphasage est égal à (180°), on dit que les signaux sont en opposition de phase. Dans cette configuration, les maximums d’un signal coïncident avec les minimums de l’autre signal ; les signaux oscillent à l’opposé l’un de l’autre.
Signaux en quadrature de phase
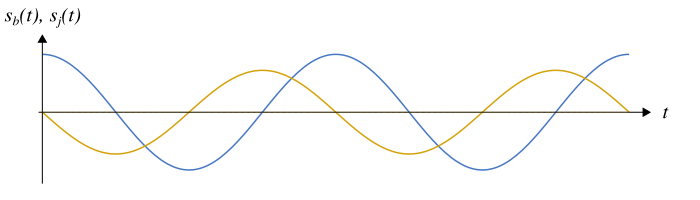
Quand le déphasage est égal à (90°), on dit que les signaux sont en quadrature de phase. Dans cette configuration, les maximums d’un signal coïncident avec les passages par zéros en décroissant de l’autre signal.
Par exemple, un signal sinusoïdal et sa dérivée sont en quadrature de phase. Le lecteur consciencieux pourra le démontrer à titre d’exercice !
Déphasage et retard temporel
Dans la première partie, nous avons évoqué le lien entre phase et avance (ou retard) temporel et ce lien se retrouve évidemment sur le déphasage. Il est ainsi possible de relier le déphasage de deux signaux de même fréquence et le retard temporel de l’un par rapport à l’autre, mais avant de faire cela, il convient de préciser un peu la notion de retard temporel.
Retard temporel
Soit deux signaux sinusoïdaux de même fréquence et pouvant s’écrire de la manière suivante :
On dira alors que est en avance (temporelle) sur de , ou, de manière équivalente que est en retard de sur .
Il faut voir comme la durée à ajouter à la variable temporelle dans l’expression de pour qu’il oscille en phase avec . De manière intuitive, cela signifie que si j’ai un maximum pour à un instant , alors j’aurai un maximum pour dans le futur, à la date .
Relation entre déphasage et retard temporel
Maintenant qu’on dispose de la notion de retard temporel, voyons comment le déphasage et le retard temporel sont liés.
Soit deux signaux et de même fréquence tels que soit déphasé de par rapport à . On peut écrire les écrire ainsi :
En factorisant partiellement par dans le cosinus, on peut transformer l’expression de en :
On peut réécrire cela sous la forme :
avec :
Nous venons d’obtenir une formule qui permet de passer d’un retard temporel à un déphasage et réciproquement.
Elle a une grande utilité pratique, notamment car de nombreux instruments permettent la mesure du temps, mais pas directement de la phase. C’est le cas notamment des oscilloscopes, très utilisés en électronique.
Considérations pratiques
Dans la pratique, l’origine des temps est une référence arbitraire (par exemple, sur un oscilloscope, le temps zéro est lié à la configuration du déclenchement). On s’intéresse en conséquence assez peu aux valeurs des phases à l’origine, et la définition du déphasage comme différence entre les phases à l’origine n’a pas d’utilité pratique. À la place, on mesure le retard pour en déduire le déphasage avec la formule vue ci-avant !
La mesure de déphasage d’un signal 2 par rapport à un signal 1 s’effectue ainsi :
- On prend un instant de référence sur le signal 1 (parce qu’on s’intéresse au déphasage du signal 2 par rapport au signal 1). Il peut s’agir par exemple d’un instant où le signal est maximum ou minimum.
- On cherche un instant analogue sur le signal 2. Par exemple, si vous avez choisi un maximum comme point de référence, il vous faut un maximum. Attention, il ne faut pas choisir n’importe quel instant analogue, mais celui le plus près de votre instant de référence. Il s’agit d’une convention qui revient à considérer le déphasage comme compris entre et .
- On mesure le retard du signal 2 par rapport au signal 1, défini par .
- On en déduit le déphasage grâce à la formule .
Cette méthode donne directement le déphasage entre les deux signaux, sans passer par les phases à l’origine.
Exercices
Exercice 1
Énoncé
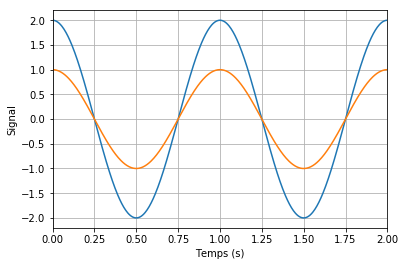
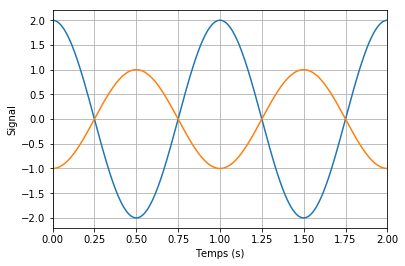
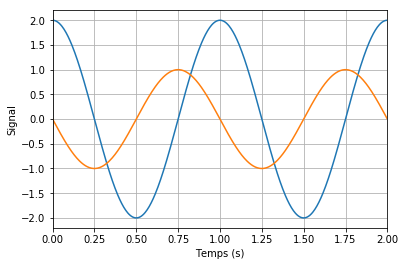
Pour chacun des cas suivants, dites si les signaux sont en opposition de phase, en quadrature de phase ou en phase.
Solution
Avant de parler de déphasage, il convient de vérifier que les signaux ont la même fréquence, ce qui est le cas.
Cas 1 : Les extremums (maximums ou minimums) coïncident : les signaux sont en phase.
Cas 2 : Les maximums coïncident avec les minimums : les signaux sont en opposition de phase.
Cas 3 : Les extremums coïncident avec les passages par zéro : les signaux sont en quadrature de phase.
Exercice 2
Énoncé
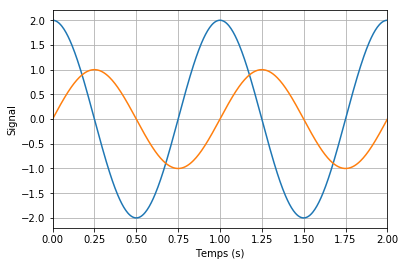
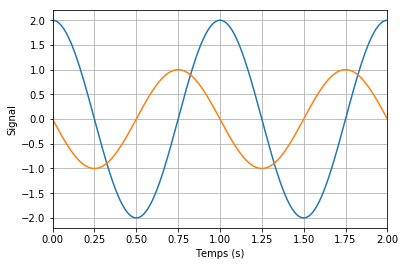
Pour chacun des cas suivants, déterminez si le signal orange est en avance ou en retard de phase par rapport au signal bleu.
Solution
Avant de parler de déphasage, il convient de vérifier que les signaux ont la même fréquence, ce qui est le cas.
Cas 1 : On peut prendre le maximum du signal bleu au centre de la figure comme référence. Le maximum du signal orange le plus proche est sur sa droite, ce qui signifie que la phase à l’origine du signal orange est plus petite que celle du signal bleu. Ainsi, le déphasage du signal orange par rapport au signal bleu est négatif et le signal orange est en retard de phase par rapport au signal bleu.
Cas 2 : Cette fois-ci, le maximum du signal orange le plus proche est sur la gauche de la référence, ce qui signifie que la phase à l’origine du signal orange est plus grande que celle du signal bleu. Ainsi, le déphasage du signal orange par rapport au signal bleu est positif et donc le signal orange est en avance de phase par rapport au signal bleu.
Exercice 3
Énoncé
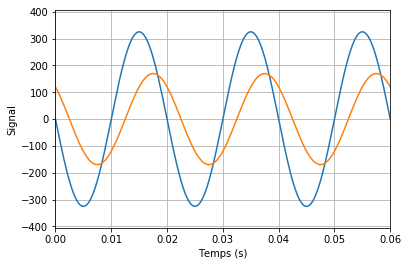
Déterminez le déphasage du signal orange par rapport au signal bleu. Faites bien attention au signe.
Solution
Avant tout, il convient de vérifier que les signaux ont la même fréquence, ce qui est le cas.
Nous allons procéder en mesurant d’abord le retard temporel du signal orange par rapport au signal bleu, puis la fréquence des signaux, et enfin en déduire le déphasage.
La première étape est de considérer si le signal orange est en avance ou en retard temporel sur le signal bleu. Comme il est à sa droite, on peut conclure que le signal orange est en retard sur le signal bleu. Son déphasage sera donc négatif.
La deuxième étape consiste à mesurer l’écart temporel. Le passage par zéro est l’endroit ou le retard est le plus facile à mesurer. C’est assez peu évident à mesurer sur une petite figure, mais l’écart entre les deux signaux vaut 1/4 de graduation, soit 2,5 ms. Le signe est négatif, car le signal orange est en retard.
Il est assez facile de voir qu’une période dure deux graduations, soit 20 ms.
On peut en déduire la fréquence :
On peut maintenant utiliser la formule qui permet de transformer un déphasage en retard et vice-versa :
Le déphasage du signal orange par rapport au signal bleu est donc de .
Ce tutoriel s’achève ici, mais sachez qu’il reste beaucoup à explorer maintenant que vous connaissez l’essentiel sur les signaux sinusoïdaux.